Chemiczne wieści (3.)

Tlen na komecie
Misja Rosetta badająca kometę 67/P Churymov-Gerasimenko budzi dziś mniejsze zainteresowanie, zwłaszcza od czasu nieszczęśliwie przedwczesnego końca lądownika, niemniej instrumenty sondy wciąż wysyłają ciekawe dane. Najnowsza publikacja Nature donosi o wykryciu w gazach wytryskujących z powierzchni jądra kometarnego molekularnego tlenu.

Jednym z instrumentów badawczych sondy jest spektrometr masowy ROSINA-DFMS. Przyrząd ten jonizuje gazy i wykrywa masy składających się nań cząsteczek, wykorzystując skłonność jonów do ruchu w polu elektrycznym z prędkością zależną od stosunku masy do ładunku. Dzięki temu możliwa jest szybka identyfikacja składu.
Dzięki niemu wiadomo było, że większość składu gazów emitowanych przez jądro kometarne (do 95%) stanowiła para wodna oraz tlenek i dwutlenek węgla. Bardziej interesujące okazały się składniki stanowiące resztę. Głównym okazał się być cząsteczkowy tlen, po nim elementarna siarka i metanol, ponadto ślady tlenków azotu i hydrazyny.

Skąd jednak tlen na komecie?
Jego zawartość porównano ze stężeniem dwutlenku węgla, tlenku i pary wodnej, wykazując że tylko w tym trzecim przypadku zachodzi wyraźna korelacja stężeń. Jeśli stężenia tlenu są powiązane ze stężeniami wody, to widocznie gazy te uwalniane są razem. Najprawdopodobniej promieniowanie ultrafioletowe wywołuje radiolizę lodu wodnego na powierzchni komety, powodując powstanie tlenu, który miesza się z lodem i wraz z nim sublimuje. Zachodzenie takiej reakcji potwierdzono zresztą eksperymentalnie. [1]

Fraktalne trójkąty
Fraktale to struktury samopodobne. Matematycznie ujmując, strukturę opisuje pewien prosty algorytm, którego nieskończone iteracje tworzą coraz mniejsze elementy, zachowujące podobieństwo do całości. Ta prostota sprawiająca, że rozległy i wydawałoby się skomplikowany wzór da się wywieść z kilku powtarzanych wciąż reguł sprawia, że struktury fraktalne bardzo często pojawiają się w przyrodzie, jako podstawa dla na przykład organizacji kolonii, układu żyłkowania liści, rozkładu pierzastych listków paproci czy form krystalicznych.

Jednym z pierwszych opisanych matematycznie fraktali, jest trójkąt Sierpińskiego. Ten polski matematyk zaproponował w 1915 roku figurę, otrzymaną wedle następującego algorytmu:
- Weź trójkąt równoboczny i łącząc środki boków podziel go na cztery mniejsze trójkąty
- Usuń trójkąt w środku
- Podziel w taki sam sposób trójkąty które pozostały
- Usuń trójkąciki po środku
- Powtórz operację w nieskończoność.

Wydawałoby się że w takiej sytuacji nic na z tego trójkąta powinno nie pozostać, w rzeczywistości jednak, ponieważ operujemy tutaj matematycznie na figurach teoretycznych, po nieskończonych podziałach i usuwaniach trójkątów otrzymamy zbiór punktów matematycznych o charakterystycznym, stałym układzie, który powtarza się w kolejnych powiększeniach w dowolnym miejscu tego trójkąta. Pole takiej figury jest zerowe.

Później wymyślono jeszcze inne podobne figury, jak dywan Sierpińskiego oparty o kwadraty, czy też bardziej dziś znane drzewkowate fraktale używane do tworzenia pięknych grafik komputerowych.

Ale co to ma wspólnego z chemią?  Otóż chemicy od dawna zastanawiali się nad produkcją materiałów o strukturze fraktalnej. Jednym z rozwiązań są dendrymery, czyli cząsteczki o wielu rozgałęzieniach, które rozgałęziają się na mniejsze rozgałęzienia a te na jeszcze mniejsze i tak dalej dopóki tylko atomy gałązek jeszcze się w kolejnej warstwie mieszczą. Cząsteczki takie mają formę kulek, których modele przypominają nieco skonfundowanego jeża. Ta oparta jest o etylenodiaminę i amid kwasu propanowego:

Dendrymery bada się obecnie intensywnie pod kątem użycia jako nośniki leków, zewnętrzna warstwa gałązek tworzy bowiem powłoczkę z małymi porami, lecz wewnątrz pojawiają się znaczne, puste przestrzenie w których umieścić można pewną ilość potrzebnej substancji, jaką należy przetransportować w organizmie w pewne określone miejsca.
Tym ciekawsze są próby stworzenia płaskiej cząsteczki o strukturze Trójkąta Sierpińskiego.

Pierwszym takim doniesieniem była obserwacja struktur w pewnym stopniu podobnych do tego fraktala w agregatach DNA na odpowiednim podłożu. Fragmenty DNA ukształtowane w formie molekularnych płytek łączyły się końcami tworząc wzór, który badano mikroskopem sił atomowych.[2]
W zeszłym roku dwaj badacze z UMCS przedstawili symulacje, pokazujące że struktury Trójkąta Sierpińskiego powinny powstawać w warstwach zawierających sztywne cząsteczki organiczne zgięte pod odpowiednim kątem i łączące się na obu końcach za pośrednictwem jonów metalu, jako wynik spontanicznej samoorganizacji.[3]
Pomysł ten okazał się chyba bardzo obiecujący, skoro wyraźnie opierają się na nim najnowsze doniesienia. Najpierw podano informację o tym, że kompleksy terpirydyny z jonami miedzi tworzą struktury stanowiące fragment trójkąta Sierpińskiego.[4] W marcu pojawiła się praca chińskich chemików opisujących tworzenie się rozległych płatów fraktalnego wzoru w wyniku osadzania na powierzchni srebra dwóch podstawowych "cegiełek" - pochodnej terfenylu, z trzema pierścieniami benzenowymi połączonymi wiązaniem w zagiętą cząsteczkę i dwoma atomami bromu na końcach; oraz pochodnej kwaterfenylu zawierającej jeden pierścień benzenu więcej. Cząsteczki te łączyły się ze sobą przez oddziaływania między bromem a wodorem.[5]
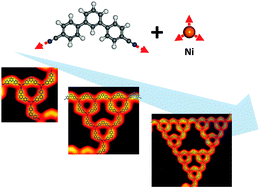
Najnowsza praca opisuje płaty kompleksów dwunitrylu terfenylu z niklem na powierzchni srebra, w których pojawiają się płaty wzoru Trójkąta Sierpińskiego. [6]

Barwnik z ery jurajskiej
Skamieniałości dawnych zwierząt i roślin w większości wyglądają jak specyficznie ukształtowana skała, są szare, białe, niekiedy opalizują jak perła. Dlatego zachowanie się pewnych barwników sprzed milionów lat stanowi ciekawy przypadek. Tak jest ze skamieniałościami wymarłych jurajskich alg Solenopora o wapiennych skorupkach, które tworzyły gąbczaste kolonie, z czasem kamieniejące, z przerastającymi rocznymi warstwami. W przypadku niektórych okazów daje się zauważyć wyraźne różowe zabarwienie, będące najwyraźniej pozostałościami pierwotnego pigmentu. W niedawno opublikowanej pracy zbadano właściwości tego barwnika, stwierdzając że to bardzo nietypowa substancja.

Barwnik otrzymany ze skamielin Solenopora jurassica sprzed około 150 milionów lat, składa się z dwóch fragmentów węglowodorowych, stanowiących najwyraźniej nie znaną pochodną antybiotyku klostrubiny A (clostrubin A) i połączonych przez atom boru ugrupowaniem spiroboranowym. Związki organiczne zawierające bor są w naturze ogółem dosyć rzadkie.
Klostrubina jest antybiotykiem wykazującym aktywność przeciwko wielu szczepom odpornych drobnoustrojów i dlatego wzbudza duże nadzieje. Jest substancją poznaną całkiem niedawno, wyizolowaną w zeszłym roku z bakterii z rodzaju Clostridium.  Duże podobieństwo struktur nowego antybiotyku i cząsteczki skamieniałego barwnika, nazwanego borolitochromem (czyli dosłownie borowym barwnikiem kamieni) jest o tyle ciekawe, że dotyczy różnych grup organizmów. Najwyraźniej geny odpowiedzialne za syntezę od dawna krążą w ekosystemie, gdzieniegdzie ujawniając się wyraźnie.
[7]

Borolitochrom i skała z której go otrzymano.

Ile atomów tworzy metal?
Wraz z przyjęciem i potwierdzeniem atomowej teorii budowy materii, chemicy i fizycy o bardziej filozoficznym zacięciu zaczęli zastanawiać się nad w sumie dość oczywistym pytaniem - ile potrzeba atomów bądź cząsteczek, aby z materii utworzyć materiał? Pojedynczy atom węgla ma inne właściwości niż choćby najmniejszy diament, trudno jest jednak wskazać moment, gdy następuje to przejście. Jest to swoisty odpowiednik "paradoksu łysego" - dwa stany skrajne, to jest łysina i pełne owłosienie, są od siebie bardzo wyraźnie różne; zarazem jednak jeśli osobie o pełnym owłosieniu zaczną pojedynczo wypadać włosy, trudno będzie nam wyznaczyć dokładną granicę od kiedy można już mówić o łysinie a kiedy jeszcze jest to tylko przerzedzenie włosów.
Ostatnie badania klastrów atomów metali pokazują jednak, że granicę naszej niepewności można w dużym stopniu zawęzić.

Metale to substancje stałe charakteryzujące się obecnością swobodnych elektronów poruszających się po sieci krystalicznej i tworzących wspólną, dużą chmurę elektronową. Właśnie dlatego metale dobrze przewodzą ciepło i elektryczność oraz odbijają światło ze srebrzystym, metalicznym połyskiem. Odpowiednio duże skupiska atomów metali też będą tworzyły swoją chmurę elektronową ale już pozostałe właściwości metaliczne niekoniecznie mogą być realizowane. Bardzo małe klastry zachowują się jak cząsteczki jakiegoś związku, często wykazując dość nieoczekiwane właściwości, przykładowo klastry 13 atomów glinu zachowują się jakby były atomem halogenku, mogąc oddawać elektrony i tworzyć aniony.

Fińscy chemicy z Uniwersytetu Jyväskylä badali takie właśnie graniczne klastry atomów złota, sprawdzając w jaki sposób reagują ze światłem. Klastry małe, mniejsze niż 102 atomy, zachowywały się jak cząsteczki. Pod wpływem fotonów przybierały pewne stany energetyczne obejmujące cały klaster, a wypromieniowanie i rozproszenie energii następowało stosunkowo (jak na atomową skalę) wolno. Grupy powyżej 144 atomów zachowywały się tak jak makroskopowe kawałki metalu, to jest szybko rozpraszały energię padającego światła, odbijały je zgodnie z prawem odbicia od lustra i nie przyjmowały ogólnoklastrowych stanów energetycznych.
Różnica była dość drastyczna - klastry większe o 42 atomy rozpraszały energię fotonów 100 razy szybciej. Natomiast klastry o wielkościach pośrednich wykazywały pośrednie własności, szybko zmieniające się z dodawaniem kolejnych atomów.
Tym samym w pewnym stopniu możliwe staje się wyznaczenie granicy między światem praw kwantowych a światem zjawisk fizyki klasycznej.[8]

-------------------
Źródła:
[1] A Bieler et al, Nature, 2015, DOI: 10.1038/nature15707
[2] Paul W K Rothemund, Nick Papadakis, Erik Winfree; Algorithmic self-assembly of DNA Sierpinski triangles. PLoS Biol 2004 Dec 7;2(12):e424. Epub 2004 Dec 7. [Open Acces]
[3] D. Nieckarz, P. Szabelski; Simulation of the self-assembly of simple molecular bricks into Sierpiński triangle,  Chem. Commun., 2014,50, 6843-6845
[4] Rajarshi S. et al.;  One-step multicomponent self-assembly of a first-generation Sierpiński triangle: from fractal design to chemical reality. Angew Chem Int Ed Engl 2014 Nov 11;53(45):12182-5.
[5] Shang J. et al.; Assembling molecular Sierpiński triangle fractals, Nature Chemistry 7, 389–393 (2015) 
[6] Sun Q. et al.; On-surface construction of a metal–organic Sierpiński triangle, Chem. Commun., 2015,51, 14164-14166
[7] Klaus Wolkenstein et al. Structure and Absolute Configuration of Jurassic Polyketide-Derived Spiroborate Pigments Obtained from Microgram Quantities, J. Am. Chem. Soc., 2015, 137 (42), pp 13460–13463 (2015).[Open Access]
[8] Mustalhi S. et al.; Molecule-like Photodynamics of Au₁₀₂(pMBA)₄₄ Nanocluster, ACS Nano, 2015, 9 (3), pp 2328–2335

Wykresy

Częstym zadaniem na zajęciach z chemii, jest wykonanie wykresu na podstawie wyników doświadczenia. Pomyślałem, że można by podać tu parę przykładów, które mogą nieco pomóc zrozumieć o co chodzi, tym niespecjalnie zaznajomionym z matematyką.

Krzywa miareczkowania

Istnieje wiele typów miareczkowań, wszystkie jednak charakteryzują się bardzo podobnym kształtem wykresu pX od objętości dodawanego odczynnika (owym X może być stężenie jonów wodorowych bądź innych). Wykres zależności logarytmu zmiennej od objętości zwykle przyjmuje postać rozciągniętej litery S, o spłaszczonych końcach i nagłym skoku wartości. Punkt końcowy takiego miareczkowania powinien znajdować się dokładnie w połowie skoku krzywej. Aby ją wyznaczyć należy zastosować dość skomplikowaną konstrukcję matematyczną, którą narysowałem na wykresie z miareczkowania potencjometrycznego, które kiedyś wykonywałem:
Należy wybrać z prostoliniowych odcinków wykresu dwie linie równoległe i znaleźć linię do nich prostopadłą. Od jej środka należy wyprowadzić linię prostopadłą. Przetnie ona skok krzywej dokładnie w połowie. Powinna przynajmniej. Można wykonywać te operacje na wydruku, linijką i cyrklem dla lepszej dokładności. Jak jednak zauważyłem, można uzyskać ten sam efekt w inny sposób, mianowicie każąc Excelowi narysować linię trendu. Przetnie ona skok krzywej w połowie, jak to widać na mojej zupełnie wymyślonej krzywej poniżej:
Sprawdzałem, że nawet trzykrotne przedłużenie jednego z prostoliniowych odcinków wykresu, nie przesuwa tego punktu, może to być zatem taki nieklasyczny sposób wyznaczenie P.K.

Inny sposób to wykreślenie wykresu pochodnej. Pochodna, to taka funkcja, która pokazuje jak szybko zmienia się funkcja dana, albo ściślej, jest to funkcja różnicy Y do X. W tym przypadku może to być delta pH do czasu. Aby zrobić to w Excelu należy wpisać w jedno z okienek taki wzór, aby uzyskać ciąg wyników odejmowań wartości pH od tej która ją poprzedza.
Może objaśnię to na konkretnym przykładzie. Mamy taką oto tabelę danych, na podstawie której stworzyliśmy wykres ze skokiem krzywej:

Pochodna to funkcja w której zamiast kolumny wyników mamy kolumnę z różnicą między wynikiem następnym i poprzednim, więc w tym przypadku odejmujemy pierwszą wartość pH od drugiej, i wpisujemy na drugie miejsce nowej kolumny (od pierwszego wyniku nie ma od czego odjąć); na trzecim miejscu będzie wynik odejmowania drugiego wyniku od trzeciego, na czwartym trzeciego od czwartego itd. Najlepiej wpisać od razu formułę i przeciągnąć w dół:

Po czym należy stworzyć nową tabelę na podstawie otrzymanych wyników:

Jak widać dopóki odejmowane od siebie wyniki mieściły się na prostej, ich pochodna przyjmowała stałą wartość, dopiero w obrębie skoku krzywej zwiększała się. Czubek "piku" pochodnej stanowi środek skoku krzywej a więc też punkt końcowy. Dla pierwszej zmyślonej krzywej:


Jeśliby jednak wartość skoku krzywej była mała a on sam dosyć łagodny, tak że nasza pochodna uzyskałaby kształt mocno zaokrąglony, dla pewności można wyprowadzić pochodną naszej pochodnej, która nam te zmiany zaostrzy. Niestety dla niedokładnych pomiarów, w których krzywa pierwotnego wykresu ma dosyć dużo nagłych załamań, będących punktami szybszej zmiany wartości, wykres drugiej pochodnej może być prawie nieczytelny, jak na tym, będącym drugą pochodną rzeczywistej krzywej z pierwszego obrazka:


Nieco inny kształt ma krzywa dla miareczkowania konduktometrycznego. Tutaj miareczkujemy analit roztworem, zawierającym jony "niwelujące" przewodnictwo związane z jonami analitu. Na przykład miareczkowanie wodorotlenku sodu kwasem solnym.
Roztwór na początku ma dobre przewodnictwo związane z obecnością kationów sodowych ale zdecydowanie mocniej z jonami hydroksylowymi. Gdy dodamy do niego kwasu solnego jony hydroksylowe zareagują z hydroniowymi czyli zobojętnią się i powstanie słabo przewodząca woda. Wprawdzie równocześnie wprowadziliśmy aniony chlorkowe, ale ich wpływ na przewodzenie nie jest duży a całość nam się rozcieńczyła dlatego ogólne przewodnictwo spadło. W miarę dodawania kolejnych porcji kwasu przewodnictwo będzie spadało aż do punktu końcowego, czyli zobojętnienia. Po jego minięciu jony hydroniowe z kwasu będą poprawiały przewodnictwo, które będzie rosło. W dobrych warunkach otrzymamy ładny wykres w kształcie litery V jak na tym z rzeczywistego miareczkowania:

Oczywiście mówię tu o dobrych warunkach, często, zwłaszcza dla miareczkowania słabych elektrolitów, krzywa jest mniej lub bardziej wypłaszczona na dnie.


Krzywa wzorcowa
Dla wielu przypadków nie możemy otrzymać wyniku pomiaru wprost, lecz musimy odnosić go do pewnej skali, wykonanej w tych samych warunkach, na przykład przez pomiar wykonany na roztworach wzorcowych o znanym stężeniu. Z każdego pomiaru otrzymujemy jeden wynik, jeden punkt do umieszczenia na wykresie. Teraz więc powinniśmy wyznaczyć z tego krzywą - albo raczej prostą. Rzecz bowiem w tym że najlepiej gdy nasz wynik mieści się w tym zakresie warunków, w którym zależność stężenie/wynik jest liniowa, wówczas możemy bez problemu przyjąć że nawet jeśli nasz wynik odpowiada położeniu między punktami roztworów wzorcowych, to odpowiada stężeniu leżącemu na wyznaczonej przez nie prostej.
Jeśli wszystko przygotujemy jak trzeba a sprzęt będzie działał bez zarzutu, otrzymamy ładniutką linię jak tu:

Niestety świat nie jest idealny a nasza dokładność ograniczona, toteż zwykle otrzymujemy pewien zbiór punktów które nie bardzo da się na siebie nałożyć. W dodatku wcale nie jest powiedziane, że zależność pomiar/stężenie musi być liniowa dla wszystkich warunków. Weźmy na przykład taki wykres zależności absorbancja/stężenie dla pewnego kompleksu:

Dla niskich stężeń kompleks jest mało trwały i zabarwienie jest słabsze niż by to wynikało z rozcieńczenia; po przekroczeniu pewnej granicy zależność jest liniowa i daje się opisać pewnym wzorem matematycznym, natomiast powyżej pewnego stężenia jony kompleksu tworzą konglomeraty zabarwione silniej. W dodatku w roztworze nie zawierającym kompleksu przyrząd zmierzył jakaś absorbancję i wykres nie zaczyna się w punkcie 0/0. Tak się akurat może zdarzyć i zdarzało się, chociaż powyższy wykres został wymyślony.
Teraz próbujemy za pomocą tego wykresu wyznaczyć z absorbancji trzech próbek ich prawdziwe stężenia - dla punktu 1 jest to łatwe, bo nałożył się na jeden z punktów pomiarowych, w tym przypadku odpowiadając stężeniu 0,09. Dla punktu 2 też nie jest to trudne - zmieścił się w zakresie zaznaczonego na czerwono odcinka liniowego, możemy więc wyznaczyć właściwe stężenie metodą graficzną, zaznaczając punkt na wykresie i sprawdzając jakiemu stężeniu odpowiada (powiedzmy że 0,055), możemy też jednak zrobić rzecz dokładniej.
Możemy wyciąć z wpisanej w Excela tabeli kawałek, odpowiadający liniowej zależności i po stworzeniu na jego podstawie wykresu kazać programowi aby wyrysował linię trendu z równaniem określającym zależność X od Y - w tym przypadku równanie miało postać Y = 8,109x + 0,928. Wiedząc jakie jest Y (absorbancja) możemy wyliczyć X czyli stężenie i równanie będzie pasowało dla wszystkich pomiarów mieszczących się w tym zakresie.
Pozostał nam jednak jeszcze jeden pomiar, który wypadł poza odcinkiem liniowym, w dodatku między punktami pomiarowymi. Możemy wykreślić między nimi odcinek i założyć, że gdy postawimy nasz punkt na tej linii to będziemy mogli odczytać prawidłową wartość, ale któż mógłby nam zaręczyć, że akurat na tym odcinku prawdziwa zależność nie wije się wedle pewnej nieprostej linii, nie poddającej się opisowi przez równania? Na przykład takiej oznaczonej zieloną krzywą. Nikt nie może czegoś takiego przewidzieć, a jeśli nie wiemy dokładnie jaka jest tutaj zależność i jakiemu Y odpowiada jaki X to nie wyznaczymy zależności ani graficznie ani matematycznie zaś wynik który możemy otrzymać będzie obarczony błędem, który może być największym błędem w całej analizie. Dlatego właśnie najlepiej wyznaczyć krzywą przed właściwym badaniem i starać się aby stężenia analizowanych próbek w miarę możliwości mieściły się w odpowiednim zakresie.

Wprowadźmy jednak nieco więcej chaosu. Może się zdarzyć że nasz sprzęt jest stary i zdarzają mu się duże szumy, zafałszowujące wyniki w obie strony i gdy naniesiemy punkty na wykres otrzymamy taką rozsypkę:

No cóż, bywa i tak. Jeśli jednak faktycznie są to przypadkowe szumy, to pamiętajmy że przypadek szumi średnio statystycznie po równo w obie strony - zatem w tym obłoczku jest prawdziwa linia trendu, a tylko złośliwie ktoś po przesuwał część punktów nad i pod nią. W takiej sytuacji musimy albo zdać się na opcję "dodaj linię trendu" albo samemu wyznaczyć jakąś linię, która znajdzie się najbardziej pomiędzy punktami. Dobra linia powinna przechodzić przez możliwie najwięcej punktów oraz umiejscawiać się pośrodku między skrajami grupy, a także mieć w miarę możliwości tyle samo punktów nad co pod nią, jak w tym przypadku:

gdzie linia przechodzi wprawdzie tylko przez trzy punkty, ale ma równo po cztery nad sobą i pod.
Ale oczywiście - powiecie zaraz,  chyba łatwiej jest zlecić to Excelowi? Jak najbardziej, tylko że czasem rzucając mu surowe dane otrzymamy linię trendu zupełnie fantazyjną, jak na poniższym przykładzie:

Zdawałoby się że wyszłaby nam ładna linijka z małymi odchyleniami, ale jeden punkt ma wartość prawie dwa razy za dużą, dlaczego? A bo na przykład obluzował się kabelek przy elektrodzie, albo kuweta kolorymetru nie była przetarta i na drodze wiązki znalazła się rozpraszająca kropla. Tak się może zdarzyć, jeśli zauważymy rzecz w porę, będziemy mogli powtórzyć pomiar tej próbki, jeśli tego nie zrobimy pozostaniemy z bardzo dziwnym wynikiem.
Jedną z rzeczy które prowadzący bardzo tępili było takie właśnie bezrefleksyjne działanie, ślepe zawierzenie procedurze, jakie obrazuje powyższy wykres. Nie trzeba wielkiego doświadczenia aby zauważyć, że z linią trendu jest coś nie tak. Wprawdzie program wyrysował ją poprawnie i zgodnie z zasadą "najbardziej wypośrodkowanej linii" ale przecież leży na niej tylko jeden punkt a zupełnie pominięto kilka leżących na wyraźnej prostej. Niestety bywało (a nawet i mi dawniej się przydarzało) że uczeń zgodnie z procedurą w ćwiczeniu tworzył wykres, kazał rysować programowi absurdalny trend, potem równanie i z równania wychodziły mu wyniki z błędem rzędu 150% i więcej. I co teraz z tym zrobić?
Do śmieci. Jeśli widzimy że wynik jest absurdalnie za duży lub za mały i występuje sam jeden dziwak wśród innych normalnych, to pomińmy go jako błąd i wyrysujmy wykres dla pozostałych danych, z czego na przykład otrzymamy coś takiego:

I od razu lepiej. Z reguły w pomiarach posiadających bardzo dużo punktów pomiarowych takie przypadkowe szumy można eliminować odpowiednimi programami, należy jedynie określić jakiś przedział, w ramach którego wyniki uznaje się za błąd, na przykład zależność powinna być liniowa i punkty odbiegające od sąsiednich - poprzedniego i następnego - o więcej niż powiedzmy 5% są eliminowane, zaś te z mniejszym odchyleniem włączane i uwzględniane. W ten sposób wykres się nam wygładza a błąd zmniejsza.
Praktyka ta ma jednak swoją złą stronę - pod pozorem eliminowania punktów błędnych nieuczciwi badacze (i studenci) mogą dopasować dane do z góry powziętej tezy. Jeśli ktoś chce wykazać silną zależność na przykład między dawką leku a spadkiem odczuwalnego stopnia bólu głowy, może wyeliminować z części wykresu dolne punkty, z drugiej górne i prowadząc trend po punktach skrajnych wykazać silne działanie preparatu. Zwykle wykrywa się takie oszustwa przez dokładną analizę - jeśli na przykład w badaniu wykazano silną korelację między podlewaniem krzewów kawowych krowim moczem a spadkiem aflatoksyn w ziarnach, lecz zarazem jako błędne wyeliminowano 40% danych, to coś tu jest nie tak.

Może coś to pomoże.

ps. ponieważ ostatnio ten post miał spore zainteresowanie, dodałem praktyczny przykład postępowania.