Kiedyś w laboratorium (18.)

Na zajęciach z chemii fizycznej w zeszłym roku, badaliśmy ruchliwość koloidu w polu elektrycznym:

Był to koloid jodku srebra. Należało nalać go do rurki tak, aby roztwór podzielił się na dwie wyraźnie odgraniczone warstwy - z koloidem i bez. Po włączeniu prądu cząstki koloidu zaczęły migrować zgodnie z ładunkiem potencjału na granicy faz, co dało się zauważyć jako zmiana poziomów. Na trzecim zdjęciu pierwsze cząstki koloidu dotarły już do elektrody.

ps. oczywiście "laboratorium" - nie wiem jak mogłem strzelić takiego babola z "laroratorium"

Wykresy

Częstym zadaniem na zajęciach z chemii, jest wykonanie wykresu na podstawie wyników doświadczenia. Pomyślałem, że można by podać tu parę przykładów, które mogą nieco pomóc zrozumieć o co chodzi, tym niespecjalnie zaznajomionym z matematyką.

Krzywa miareczkowania

Istnieje wiele typów miareczkowań, wszystkie jednak charakteryzują się bardzo podobnym kształtem wykresu pX od objętości dodawanego odczynnika (owym X może być stężenie jonów wodorowych bądź innych). Wykres zależności logarytmu zmiennej od objętości zwykle przyjmuje postać rozciągniętej litery S, o spłaszczonych końcach i nagłym skoku wartości. Punkt końcowy takiego miareczkowania powinien znajdować się dokładnie w połowie skoku krzywej. Aby ją wyznaczyć należy zastosować dość skomplikowaną konstrukcję matematyczną, którą narysowałem na wykresie z miareczkowania potencjometrycznego, które kiedyś wykonywałem:
Należy wybrać z prostoliniowych odcinków wykresu dwie linie równoległe i znaleźć linię do nich prostopadłą. Od jej środka należy wyprowadzić linię prostopadłą. Przetnie ona skok krzywej dokładnie w połowie. Powinna przynajmniej. Można wykonywać te operacje na wydruku, linijką i cyrklem dla lepszej dokładności. Jak jednak zauważyłem, można uzyskać ten sam efekt w inny sposób, mianowicie każąc Excelowi narysować linię trendu. Przetnie ona skok krzywej w połowie, jak to widać na mojej zupełnie wymyślonej krzywej poniżej:
Sprawdzałem, że nawet trzykrotne przedłużenie jednego z prostoliniowych odcinków wykresu, nie przesuwa tego punktu, może to być zatem taki nieklasyczny sposób wyznaczenie P.K.

Inny sposób to wykreślenie wykresu pochodnej. Pochodna, to taka funkcja, która pokazuje jak szybko zmienia się funkcja dana, albo ściślej, jest to funkcja różnicy Y do X. W tym przypadku może to być delta pH do czasu. Aby zrobić to w Excelu należy wpisać w jedno z okienek taki wzór, aby uzyskać ciąg wyników odejmowań wartości pH od tej która ją poprzedza.
Może objaśnię to na konkretnym przykładzie. Mamy taką oto tabelę danych, na podstawie której stworzyliśmy wykres ze skokiem krzywej:

Pochodna to funkcja w której zamiast kolumny wyników mamy kolumnę z różnicą między wynikiem następnym i poprzednim, więc w tym przypadku odejmujemy pierwszą wartość pH od drugiej, i wpisujemy na drugie miejsce nowej kolumny (od pierwszego wyniku nie ma od czego odjąć); na trzecim miejscu będzie wynik odejmowania drugiego wyniku od trzeciego, na czwartym trzeciego od czwartego itd. Najlepiej wpisać od razu formułę i przeciągnąć w dół:

Po czym należy stworzyć nową tabelę na podstawie otrzymanych wyników:

Jak widać dopóki odejmowane od siebie wyniki mieściły się na prostej, ich pochodna przyjmowała stałą wartość, dopiero w obrębie skoku krzywej zwiększała się. Czubek "piku" pochodnej stanowi środek skoku krzywej a więc też punkt końcowy. Dla pierwszej zmyślonej krzywej:


Jeśliby jednak wartość skoku krzywej była mała a on sam dosyć łagodny, tak że nasza pochodna uzyskałaby kształt mocno zaokrąglony, dla pewności można wyprowadzić pochodną naszej pochodnej, która nam te zmiany zaostrzy. Niestety dla niedokładnych pomiarów, w których krzywa pierwotnego wykresu ma dosyć dużo nagłych załamań, będących punktami szybszej zmiany wartości, wykres drugiej pochodnej może być prawie nieczytelny, jak na tym, będącym drugą pochodną rzeczywistej krzywej z pierwszego obrazka:


Nieco inny kształt ma krzywa dla miareczkowania konduktometrycznego. Tutaj miareczkujemy analit roztworem, zawierającym jony "niwelujące" przewodnictwo związane z jonami analitu. Na przykład miareczkowanie wodorotlenku sodu kwasem solnym.
Roztwór na początku ma dobre przewodnictwo związane z obecnością kationów sodowych ale zdecydowanie mocniej z jonami hydroksylowymi. Gdy dodamy do niego kwasu solnego jony hydroksylowe zareagują z hydroniowymi czyli zobojętnią się i powstanie słabo przewodząca woda. Wprawdzie równocześnie wprowadziliśmy aniony chlorkowe, ale ich wpływ na przewodzenie nie jest duży a całość nam się rozcieńczyła dlatego ogólne przewodnictwo spadło. W miarę dodawania kolejnych porcji kwasu przewodnictwo będzie spadało aż do punktu końcowego, czyli zobojętnienia. Po jego minięciu jony hydroniowe z kwasu będą poprawiały przewodnictwo, które będzie rosło. W dobrych warunkach otrzymamy ładny wykres w kształcie litery V jak na tym z rzeczywistego miareczkowania:

Oczywiście mówię tu o dobrych warunkach, często, zwłaszcza dla miareczkowania słabych elektrolitów, krzywa jest mniej lub bardziej wypłaszczona na dnie.


Krzywa wzorcowa
Dla wielu przypadków nie możemy otrzymać wyniku pomiaru wprost, lecz musimy odnosić go do pewnej skali, wykonanej w tych samych warunkach, na przykład przez pomiar wykonany na roztworach wzorcowych o znanym stężeniu. Z każdego pomiaru otrzymujemy jeden wynik, jeden punkt do umieszczenia na wykresie. Teraz więc powinniśmy wyznaczyć z tego krzywą - albo raczej prostą. Rzecz bowiem w tym że najlepiej gdy nasz wynik mieści się w tym zakresie warunków, w którym zależność stężenie/wynik jest liniowa, wówczas możemy bez problemu przyjąć że nawet jeśli nasz wynik odpowiada położeniu między punktami roztworów wzorcowych, to odpowiada stężeniu leżącemu na wyznaczonej przez nie prostej.
Jeśli wszystko przygotujemy jak trzeba a sprzęt będzie działał bez zarzutu, otrzymamy ładniutką linię jak tu:

Niestety świat nie jest idealny a nasza dokładność ograniczona, toteż zwykle otrzymujemy pewien zbiór punktów które nie bardzo da się na siebie nałożyć. W dodatku wcale nie jest powiedziane, że zależność pomiar/stężenie musi być liniowa dla wszystkich warunków. Weźmy na przykład taki wykres zależności absorbancja/stężenie dla pewnego kompleksu:

Dla niskich stężeń kompleks jest mało trwały i zabarwienie jest słabsze niż by to wynikało z rozcieńczenia; po przekroczeniu pewnej granicy zależność jest liniowa i daje się opisać pewnym wzorem matematycznym, natomiast powyżej pewnego stężenia jony kompleksu tworzą konglomeraty zabarwione silniej. W dodatku w roztworze nie zawierającym kompleksu przyrząd zmierzył jakaś absorbancję i wykres nie zaczyna się w punkcie 0/0. Tak się akurat może zdarzyć i zdarzało się, chociaż powyższy wykres został wymyślony.
Teraz próbujemy za pomocą tego wykresu wyznaczyć z absorbancji trzech próbek ich prawdziwe stężenia - dla punktu 1 jest to łatwe, bo nałożył się na jeden z punktów pomiarowych, w tym przypadku odpowiadając stężeniu 0,09. Dla punktu 2 też nie jest to trudne - zmieścił się w zakresie zaznaczonego na czerwono odcinka liniowego, możemy więc wyznaczyć właściwe stężenie metodą graficzną, zaznaczając punkt na wykresie i sprawdzając jakiemu stężeniu odpowiada (powiedzmy że 0,055), możemy też jednak zrobić rzecz dokładniej.
Możemy wyciąć z wpisanej w Excela tabeli kawałek, odpowiadający liniowej zależności i po stworzeniu na jego podstawie wykresu kazać programowi aby wyrysował linię trendu z równaniem określającym zależność X od Y - w tym przypadku równanie miało postać Y = 8,109x + 0,928. Wiedząc jakie jest Y (absorbancja) możemy wyliczyć X czyli stężenie i równanie będzie pasowało dla wszystkich pomiarów mieszczących się w tym zakresie.
Pozostał nam jednak jeszcze jeden pomiar, który wypadł poza odcinkiem liniowym, w dodatku między punktami pomiarowymi. Możemy wykreślić między nimi odcinek i założyć, że gdy postawimy nasz punkt na tej linii to będziemy mogli odczytać prawidłową wartość, ale któż mógłby nam zaręczyć, że akurat na tym odcinku prawdziwa zależność nie wije się wedle pewnej nieprostej linii, nie poddającej się opisowi przez równania? Na przykład takiej oznaczonej zieloną krzywą. Nikt nie może czegoś takiego przewidzieć, a jeśli nie wiemy dokładnie jaka jest tutaj zależność i jakiemu Y odpowiada jaki X to nie wyznaczymy zależności ani graficznie ani matematycznie zaś wynik który możemy otrzymać będzie obarczony błędem, który może być największym błędem w całej analizie. Dlatego właśnie najlepiej wyznaczyć krzywą przed właściwym badaniem i starać się aby stężenia analizowanych próbek w miarę możliwości mieściły się w odpowiednim zakresie.

Wprowadźmy jednak nieco więcej chaosu. Może się zdarzyć że nasz sprzęt jest stary i zdarzają mu się duże szumy, zafałszowujące wyniki w obie strony i gdy naniesiemy punkty na wykres otrzymamy taką rozsypkę:

No cóż, bywa i tak. Jeśli jednak faktycznie są to przypadkowe szumy, to pamiętajmy że przypadek szumi średnio statystycznie po równo w obie strony - zatem w tym obłoczku jest prawdziwa linia trendu, a tylko złośliwie ktoś po przesuwał część punktów nad i pod nią. W takiej sytuacji musimy albo zdać się na opcję "dodaj linię trendu" albo samemu wyznaczyć jakąś linię, która znajdzie się najbardziej pomiędzy punktami. Dobra linia powinna przechodzić przez możliwie najwięcej punktów oraz umiejscawiać się pośrodku między skrajami grupy, a także mieć w miarę możliwości tyle samo punktów nad co pod nią, jak w tym przypadku:

gdzie linia przechodzi wprawdzie tylko przez trzy punkty, ale ma równo po cztery nad sobą i pod.
Ale oczywiście - powiecie zaraz,  chyba łatwiej jest zlecić to Excelowi? Jak najbardziej, tylko że czasem rzucając mu surowe dane otrzymamy linię trendu zupełnie fantazyjną, jak na poniższym przykładzie:

Zdawałoby się że wyszłaby nam ładna linijka z małymi odchyleniami, ale jeden punkt ma wartość prawie dwa razy za dużą, dlaczego? A bo na przykład obluzował się kabelek przy elektrodzie, albo kuweta kolorymetru nie była przetarta i na drodze wiązki znalazła się rozpraszająca kropla. Tak się może zdarzyć, jeśli zauważymy rzecz w porę, będziemy mogli powtórzyć pomiar tej próbki, jeśli tego nie zrobimy pozostaniemy z bardzo dziwnym wynikiem.
Jedną z rzeczy które prowadzący bardzo tępili było takie właśnie bezrefleksyjne działanie, ślepe zawierzenie procedurze, jakie obrazuje powyższy wykres. Nie trzeba wielkiego doświadczenia aby zauważyć, że z linią trendu jest coś nie tak. Wprawdzie program wyrysował ją poprawnie i zgodnie z zasadą "najbardziej wypośrodkowanej linii" ale przecież leży na niej tylko jeden punkt a zupełnie pominięto kilka leżących na wyraźnej prostej. Niestety bywało (a nawet i mi dawniej się przydarzało) że uczeń zgodnie z procedurą w ćwiczeniu tworzył wykres, kazał rysować programowi absurdalny trend, potem równanie i z równania wychodziły mu wyniki z błędem rzędu 150% i więcej. I co teraz z tym zrobić?
Do śmieci. Jeśli widzimy że wynik jest absurdalnie za duży lub za mały i występuje sam jeden dziwak wśród innych normalnych, to pomińmy go jako błąd i wyrysujmy wykres dla pozostałych danych, z czego na przykład otrzymamy coś takiego:

I od razu lepiej. Z reguły w pomiarach posiadających bardzo dużo punktów pomiarowych takie przypadkowe szumy można eliminować odpowiednimi programami, należy jedynie określić jakiś przedział, w ramach którego wyniki uznaje się za błąd, na przykład zależność powinna być liniowa i punkty odbiegające od sąsiednich - poprzedniego i następnego - o więcej niż powiedzmy 5% są eliminowane, zaś te z mniejszym odchyleniem włączane i uwzględniane. W ten sposób wykres się nam wygładza a błąd zmniejsza.
Praktyka ta ma jednak swoją złą stronę - pod pozorem eliminowania punktów błędnych nieuczciwi badacze (i studenci) mogą dopasować dane do z góry powziętej tezy. Jeśli ktoś chce wykazać silną zależność na przykład między dawką leku a spadkiem odczuwalnego stopnia bólu głowy, może wyeliminować z części wykresu dolne punkty, z drugiej górne i prowadząc trend po punktach skrajnych wykazać silne działanie preparatu. Zwykle wykrywa się takie oszustwa przez dokładną analizę - jeśli na przykład w badaniu wykazano silną korelację między podlewaniem krzewów kawowych krowim moczem a spadkiem aflatoksyn w ziarnach, lecz zarazem jako błędne wyeliminowano 40% danych, to coś tu jest nie tak.

Może coś to pomoże.

ps. ponieważ ostatnio ten post miał spore zainteresowanie, dodałem praktyczny przykład postępowania.

Co nieco o Jodzie

 Wpis początkowo mający być migawką z tego co też zdarzyło mi się kiedyś w laboratorium nieco mi się poszerzył, dlatego będzie ogólnie o jodzie i jego analityce.Na początek opowiem o pewnej często stosowanej próbie analitycznej.
Dla wykrycia w badanym roztworze jodków, za pomocą klasycznej "próbówkowej" analizy jakościowej, zazwyczaj dodaje się do niego wody chlorowej i wytrząsa z chloroformem. Chloroform nie miesza się z wodą i osiada przy dnie jako odrębna warstewka, która po wytrząśnięciu z roztworem zawierającym jod, zabarwia się na różowo:

W tym przypadku roztwór był dosyć stężony, więc kolor jest bardzo wyraźny. Widać też różnicę między kolorem wodnego i organicznego roztworu jodu. W wodzie, w której rozpuszcza się słabo, daje zabarwienie brunatne, z pomarańczowym odcieniem. Skąd ta różnica?

Aby wyjaśnić takie zachowanie trzeba zacząć od przyczyny fioletowej barwy pierwiastka, widocznej w stanie gazowym. W stanie stały większe grudki przypominają grafit o niebieskawym odcieniu, dopiero w drobnych, prześwitujących ziarnach lub właśnie oparach, widać dobrze intensywny fiolet.
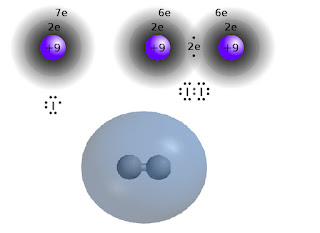
Jod tworzy cząsteczki dwuatomowe, między którymi istnieje wiązanie kowalencyjne. Wiązanie tego typu polega na połączeniu w parę po jednym wolnym elektronie z łączących się pierwiastków i umieszczeniu jej w przestrzeni między atomami. Ta "wiążące para elektronowa" oddziałuje wespół zespół z obydwoma atomami, dlatego jest dla nich "uwspólniona", zaś każdy uzyskuje w ten sposób wrażenie oktetu - najtrwalszej konfiguracji elektronów w otoczeniu. Jednakowoż jeśli opiszemy rzecz metodami mechaniki kwantowej, widzącej elektrony raczej jako rozmyte chmurki aniżeli kulki na orbitach, to rzecz stanie się nieco bardziej zawikłana.
W kwantowym modelu atomu zamiast mknących kulek mamy jak rzekłem chmurkę - a właściwie przestrzeń nazywaną orbitalem. Wiemy że elektron jest w tej przestrzeni, ale z różnym prawdopodobieństwem, co w istocie przekłada się na różne rozłożenie jego ładunku. Wiązanie pomiędzy atomami jodu tworzą zewnętrzne elektrony sigma, których orbitale są kuliste, i przez ich nakładanie się powstaje wspólny orbital molekularny obejmujący całą cząsteczkę z grubsza na kształt piłki do rugby:

Jednak sposobów łączenia się orbitali jest znacznie więcej, każdemu zaś odpowiada nieco inna energia. W tym przypadku najwyższemu rzeczywistemu orbitalowi sigma (HOMO) towarzyszy leżący nad nim najniższy potencjalny orbital (LUMO) nie zapełniony. Poziomy energetyczne tych orbitali leżą na tyle blisko, że stan elektronu może przechodzić z jednej możliwości w drugą, musi jedynie mieć dostarczoną ściśle określoną porcję energii. Na przykład może pochłonąć kwant światła odpowiadający konkretnej barwie.
Jeśli z białego światła, będącego mieszaniną wszystkich kolorów, wyciąć jakiś jeden, to suma reszty będzie widoczna jako kolor przeciwny. W tym przypadku intensywne pochłanianie zieleni, powoduje powstanie koloru fioletowego swobodnych par tego pierwiastka. Nieco inaczej rzecz przedstawia się w roztworach.

Już tu kiedyś pisałem, że w dydaktyce szkolnej opis rozpuszczania przedstawia ten proces tak, jakby zachodził w próżni, w rzeczywistości bowiem rozpuszczalnik zawsze w jakimś stopniu oddziałuje z cząsteczkami rozpuszczanych substancji. Niejednokrotnie cząsteczka zostaje otoczona warstewką silnie przyciągniętych cząsteczek rozpuszczalnika, co nie pozostaje bez wpływu na jej właściwości.
W przypadku Jodu rozpuszczalniki polarne oddziałują na tyle silnie, że tworzą kompleks, przenosząc część ładunku na jod. Poziomy energetyczne orbitali molekularnych rzeczywistego i potencjalnego rozsuwają się, jod zaczyna pochłaniać inną długość fali i zmienia kolor w stronę brunatnej czerwieni. Dlatego w wodzie i acetonie tworzy roztwory o takiej barwie. W rozpuszczalnikach słabiej oddziałujących, jak dichlorometan, jest intensywnie czerwony. W jeszcze słabszych, jak chloroform czy benzen jest różowy, a w najsłabiej oddziałujących jak heksan, tworzy roztwór fioletowy, tak jak w powietrzu. Jest to jeden z najwyraźniejszych przykładów solwatochromizmu.

Barwa skrobi zabarwionej jodem

Tak więc wyjaśniłem już o co chodzi w opisywanej próbie analitycznej. Nie jest ona zbytnio czuła i ma raczej znaczenie historyczne. Jest jednak jeszcze inna próba, bardziej dokładna i nadająca się do wykrywania śladowych ilości - mianowicie reakcja ze skrobią.
Skrobia, jak to już niedawno tłumaczyłem, jest naturalnym polimerem złożonych z połączonych w długie łańcuchy cząsteczek glukozy. Zależnie od typu łańcucha wyróżniamy prostą amylozę i rozgałęzioną amylopektynę - w przypadku tej ostatniej oddziaływania powodują, że łańcuchy te skręcają się w sprężynki.
Jod rozpuszcza się w wodzie bardzo słabo, chyba że obecne będą w niej jony jodkowe - łączy się wówczas w jony trójjodkowe, będące cząsteczkami wydłużonymi. Roztwór taki nazywa się płynem Lugola (natomiast klasyczna jodyna to roztwór w alkoholu). Tak się akurat składa, że rozmiar "sprężynki" amylozy, pasuje do wielkości cząsteczki trójjodkowej, toteż wpasowuje się ona między skręcone zwoje, tworząc dosyć trwały kompleks o intensywnym, granatowym zabarwieniu.

Barwa kompleksu zależy w pewnym stopniu od stężenia jodu - dla bardzo małych, jest granatowy, dla większych staje się brunatny do czerwonego. Barwa jest zauważalna już dla ilości 0,00002 mol/l jodu w roztworze. Tą samą metodą można wykryć jodki - same co prawda nie reagują ze skrobią, ale mogą być przeprowadzone w jod przez utlenienie. Jeśli do badanego roztworu dodamy zawiesinę skrobi i na przykład wodę chlorowa, to część jodków utleni się i powstający kompleks to uwidoczni.
Nie trudno zgadnąć, że skoro możemy skrobią wykryć jod, to i jodem możemy wykryć skrobię - i rzeczywiście, próba jodowa jest używana do sprawdzenia ilości i rozkładu skrobi w roślinach i pożywieniu. Tak można testować na przykład stopień dojrzałości jabłek - młode owoce zawierają głównie skrobię i kwasy owocowe, skąd cierpki smak młodych jabłuszek; w miarę rozwoju skrobia jest zużywana a w jej miejsce pojawia się coraz więcej cukrów, które maskują kwaśny posmak. Po przekrojeniu owocu polewa się powierzchnię płynem Lugola - zależnie od wielkości i rozmieszczenia zabarwienia przypisuje się owocom różną dojrzałość. W ten sposób można też wykryć obecność skrobi (również jej modyfikowanych chemicznie pochodnych, o których pisałem) tam gdzie znaleźć się nie powinna - na przykład przetworach mlecznych co do których producent nie deklaruje dodatków. Opisał to pięknie Stobiński w "Chemii i życiu".
Ale to nie koniec - wiemy że do reakcji potrzebne są na przykład jodki, skrobia i utleniacze, zatem mając te dwa pierwsze, możemy wykryć ten trzeci składnik.
Mogą to być gazy będące silnymi utleniaczami, jak chlor i brom, czy też ozon. Papierek jodoskrobiowy, zawierający jodki i skrobię, po zwilżeniu i przyłożeniu do wylotu próbówki z której jak sądzimy ulatniają się te gazy, pociemnieje. Profesjonalne paski testowe mają często skalę na której można w pewnym zakresie wyznaczać stężenie utleniaczy - w ten sposób sprawdza się na przykład czy ilość chloru w wodzie pitnej i kąpielowej nie przekracza norm.
Mogą to być silne utleniacze w roztworze, na przykład chlorany czy nadtlenek wodoru, tu jednak przy większych ilościach barwa może pojawić się na krótko - wydzielony jod jest dalej utleniony do bezbarwnych jodanów. Mogą to być nawet słabsze utleniacze, jeśli tylko ulegają odpowiedniej reakcji - na przykład azotyny (azotany III), w odróżnieniu od azotanów V. Reakcji z wydzieleniem jodu ulegają też niektóre metale - na przykład kationy miedzi II i żelaza III, będące raczej słabymi utleniaczami - toteż można by zapewne użyć papierków do wykrycia tych metali, ale dla nich znamy inne testy. Tą trójkę powiązaną możliwościami analitycznymi przedstawiłem na grafice:

Tak więc wiemy już jak wykryć jod i co wykryć można za jego pomocą, jest jednak jeszcze jedno zastosowanie jodu w analityce - mianowicie analiza ilościowa za pomocą miareczkowania jodometrycznego.

Cały pomysł polega na prostej zasadzie - pierwiastkowy jod łatwo redukuje się do jodków. Jeśli będziemy miareczkować jego roztwór przy pomocy roztworu reduktora o znanym stężeniu aż do zaniku barwy, to będziemy mogli ze zużytej objętości wyliczyć stężenie analitu, czyli zawartość jodu. Jeśli zaś mamy roztwór substancji reagującej z jodem o nieznanym stężeniu, to możemy dodać do niej znaną ilość jodu tak aby był to nadmiar, i zmiareczkować pozostały jod. wiedząc ile ubyło z pierwotnej ilości dodanego jodu, możemy wyliczyć ile musiało być w roztworze reagującej substancji.
Odwrotny przypadek to sytuacja gdy mamy nieoznaczony roztwór substancji mogącej utlenić jodki do wolnego jodu - dodajemy wówczas znaną ilość jodków i odmiareczkowujemy  jod powstały w reakcji.

Jako reduktora zazwyczaj używa się tiosiarczanu sodu, który reaguje szybko wedle reakcji:

 I₃^- + 2 S₂O₃^2- → S₄O₆^2- + 3 I^-

Co zaś można oznaczać? W sposób bezpośredni siarczyny, siarczki, arsen III, glukozę i kwas askorbinowy, w pośredni wolny chlor, chlorany, azotyny, sole miedzi II i żelaza III.
Tak się akurat składa, że spośród filmów miareczkowań jakie zrobiłem, najwięcej jest miareczkowań jodometrycznych i jeden z nich niedawno udostępniłem. Wykonałem go podczas praktyk w Siedleckim LOŚP, zaś analizowanym roztworem był wzorzec siarczynów:

Jest to właściwie najistotniejsza minuta miareczkowania. Ilość jodu słabnie a wraz z nią odcień roztworu. Gdy roztwór jest już słomkowy dodaję zawiesinę skrobi - dzięki temu łatwiej będzie mi uchwycić punkt końcowy, gdy zanikają ostatnie tony zabarwienia.

Ot, i tyle.

Ostatnio w laboratorium (17.)

Na ostatniej przed świętami pracowni z chemii proekologicznej, analizowaliśmy kawałki tworzyw sztucznych, aby móc poznać z jakim konkretnie tworzywem mieliśmy do czynienia. Kawałkami tymi były: pocięta folia z opakowania loda, pocięte opakowanie kremu (z etykiety wyczytałem "do rąk i do stóp"), kawałki miękkiej rurki, kawałki uszczelki, kawałki niebieskiej zakrętki od butelki wody mineralnej i kawałek zielonego plastiku z jakiegoś opakowania z gwintem.
Jednym ze sposobów rozróżnienia tworzyw, było poznanie ich gęstości metodą flotacyjną - przez sprawdzenie pływalności w różnych roztworach. Najpierw więc dzieliliśmy je na te, które pływały w widzie i te które tonęły; z tych pierwszych na te które pływały z 30% etanolu i te które tonęły, zaś z tych pierwszych sprawdzaliśmy jeszcze pływalność w 58% etanolu. I tutaj kawałeczek zielonego plastiku po wrzuceniu do roztworu opadł na dno, potem zaczął wynurzać się aż wreszcie pozostał swobodnie zawieszony mniej więcej pośrodku.:

Znaczyłoby to, że roztwór miał akurat taką samą gęstość jak ten plastik (ok. 0,88g/ml). Z drugiej strony materiał był nieprzezroczysty i zabarwiony, musiał więc zawierać wypełniacze i pigmenty, które nieco go dociążyły. A skoro tak, to bez nich pływałby.

Inne próby dotyczyły rozpuszczalności lub nie w acetonie a nasam koniec została nam próba spalania. Niektóre materiały można dosyć łatwo rozróżnić po tym jak się palą. Poliolefiny (polietylen, polibutylen) zapalają się łatwo, słabo kopcą, kapią i po zgaszeniu pachną podobnie do świecy ze stearyny. Tak też zachował się nasz kawałek zielonego plastiku:

 PCW zapala się trudno i kopci, gaśnie po wyjęciu z płomienia i wydziela nieprzyjemny, ostry zapach będący głównie wynikiem wydzielania się chlorowodoru. Polistyren pali się łatwo i silnie kopci. Jeszcze nie podsumowałem notatek i nie zrobiłem sprawozdania, więc na razie nie podam co było czym, a sam już dziś nie pamiętam.

A aspekt proekologiczny? Jeśli będziemy wiedzieli z jakiego plastiku są odpady, będziemy wiedzieli co można zakompostować, co przetopić a co wyrzucić na śmietnisko. Nie wiem jedynie czy w sortowniach stosują takie proste metody - ja bym wolał jakiś spektroskop.